“不同路径问题”是LeetCode上的一系列问题(包含第62题、第63题和第980题),本文以第62题入手记录一下解决这种问题的思路,先贴上代码实现的Github地址。
问题描述
一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为“Start” )。机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为“Finish”)。问总共有多少条不同的路径?(题目来源:力扣LeetCode)
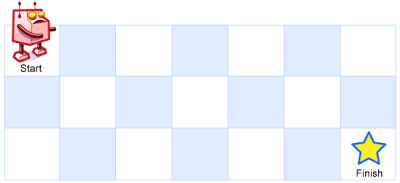
示例 1:
输入: m = 3, n = 2
输出: 3
解释:
从左上角开始,总共有 3 条路径可以到达右下角。
1. 向右 -> 向右 -> 向下
2. 向右 -> 向下 -> 向右
3. 向下 -> 向右 -> 向右
这里需要注意的是当整个网格只有一格也就是m=1,n=1时,总共可能的路径为1。
问题分析和代码实现
如果遇到这个问题前没学习过动态规划的话那么肯定一上来就是穷举法,然后ifelse写的欲仙欲死,最后时间复杂度还上天,但学习了动态规划后就知道解决这类问题有套路——先自顶向下、然后自底向上,那么对于不同路径这个问题它的顶和底都是啥呢?首先对于m*n的网格我们考虑Finish节点(其实动态规划一般都是从尾部开始考虑整个问题的),可以很容易发现总的路径条数就等于从Start节点走到Finish节点正上方节点(记为top)的条数加上从Start节点走到Finish节点左前方节点(记为left)的条数,那么走到top节点的条数又取决于从Start节点到top正上方和top左前方路径条数的和,求走到left节点的条数同理。当然这里也有边界条件,当节点处于最上边(n=1)时或最左边(m=1)时此时路径条数恒为1(题目规定只能往右边或者下边走)。我们可以使用F(m,n)代表m*n的网格所有路径条数,经过上面的分析可以得出状态转移方程如下:
F(m,n)=1;//当m=1或者n=1时
F(m,n)=F(m-1,n)+F(m,n-1);//当m>1或者n>1时
至此为止自顶向下的分析过程就完成了,接下来是编写代码了,根据状态转移方程和边界条件我们可以很容易写出如下代码:
public int uniquePaths(int m, int n) {
if(m<=0||n<=0){
return 0;
}
if(m==1||n==1){
return 1;
}
return uniquePaths(m-1,n)+uniquePaths(m,n-1);
}
上面这段代码经验证的确是没有逻辑上的问题的,并且空间复杂度为O(1),但它有一个最大的问题就是时间复杂度太高,代码执行过程如下图所示:
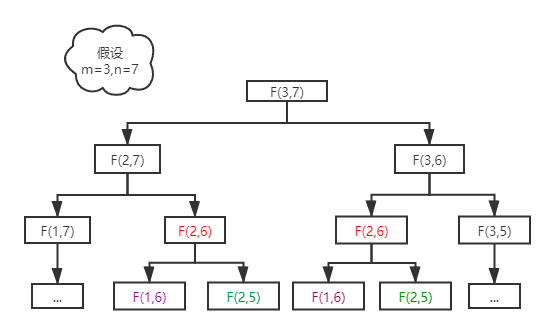
可以看到F(2,6)、F(1,6)、F(2,5)的值被重复计算了,而且代码越往下执行重复计算的次数越多,整个计算过程最后会变成一棵二叉树,时间复杂度为O(2^n)。众所周知时间复杂度为幂次方的算法都是不能上战场(工业使用)的,这段代码提交到LeetCode上系统也会提示超时,所以现在要降低重复计算的次数,可以很容易的想到使用一个二维数组arr[m][n]去保存每次计算F(m,n)后的结果,每次递归时判断arr[m][n]是否等于0,如果不等于0直接返回arr[m][n]即可,代码如下所示:
public int uniquePaths(int m, int n,int [][] arr) {
if(arr == null){
arr = new int[m][n];
}
if(arr[m-1][n-1]>0){
return arr[m-1][n-1];
}
if(m<=0||n<=0){
return 0;
}
if(m==1||n==1){
arr[m-1][n-1] = 1;
return arr[m-1][n-1];
}
arr[m-1][n-1] = uniquePaths(m-1,n,arr)+uniquePaths(m,n-1,arr);
return arr[m-1][n-1];
}
上面这种解法也称作备忘录算法,时间复杂度和空间复杂度都是O(m*n),实测在m=20、n=20的情况下,未使用备忘录的算法等了将近半分钟还没结果,但是备忘录解法在0ms内输出了结果,优化效果还是很明显的,但别高兴得太早,备忘录算法还不算真正的动态规划算法,只有自底向上递推后得到的代码才能真正算得上动态规划算法。
自底向上递推
接上述,首先假设m=3、n=7,通过上面的分析和状态转移方程,我们做一个表格如下所示(一般自底向上递推的过程用表格会很直观,表格里的数字代表从Start走到此位置的路径条数):
| 行\列 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 2 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 3 | 1 | 3 | 6 | 10 | 15 | 21 | 28 |
从表格中很容易看出当m=1或者n=1的时候,当前节点对应的路径条数为1;当m>1并且n>1时,当前节点对应的路径条数为节点正上方和节点左前方路径之和,所以不用递归就可以求出结果。
public int uniquePaths(int m, int n){
if(m <= 0 || n <= 0){
return 0;
}
int arr[][] = new int[m][n];
for(int i=0;i<m;i++){
for(int j=0;j<n;j++){
if(i == 0 || j == 0){
arr[i][j] = 1;
}else{
arr[i][j] = arr[i-1][j]+arr[i][j-1];
}
}
}
return arr[m-1][n-1];
}
通过代码可以很容易得到动态规划算法时间复杂度和空间复杂度都是O(m*n),代码结构也十分清晰。
总结
- 动态规划一般前期自顶向下得出状态转移方程、边界和最优子结构,中期通过备忘录降低时间复杂度,后期通过自底向上递推(一般使用表格分析一组数据)得到最优算法。
- 动态规划的自顶向下分析一般从转移方程最末端开始分析,直到找到状态转移方程和边界
- 动态规划只有找到了状态转移方程和边界才能真正进行编码